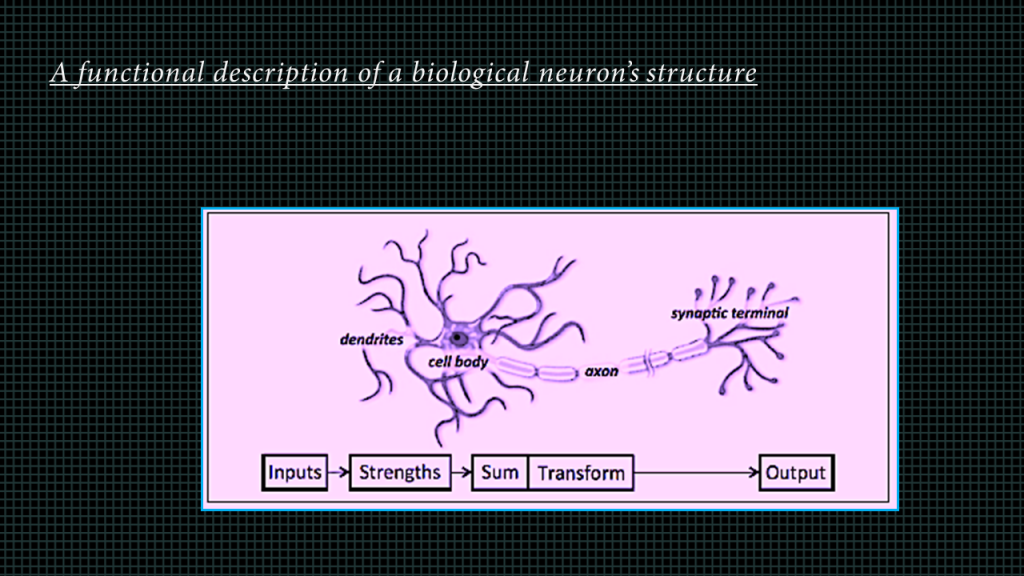
The foundational unit of the human brain is the neuron. A tiny piece of the brain, about the size of grain of rice, contains over 10,000 neurons, each of which forms an average
It’s this massive biological network that enables us to experience the world around us. of 6,000 connections with other neurons.
At its core, the neuron is optimized to receive information from other neurons, pro‐ cess this information in a unique way, and send its result to other cells a shown in this image over here.
The neuron receives its inputs along antennae-like struc‐ tures called dendrites. Each of these incoming connections is dynamically strengthened or weakened based on how often it is used (this is how we learn new concepts!), and it’s the strength of each connection that determines the contribution of the input to the neuron’s output. After being weighted by the strength of their respective con‐ nections, the inputs are summed together in the cell body. This sum is then trans‐ formed into a new signal that’s propagated along the cell’s axon and sent off to other neurons.
Now that the biological neuron is out of the way lets go back to artificial neurons.
Muscle Gain Predictor
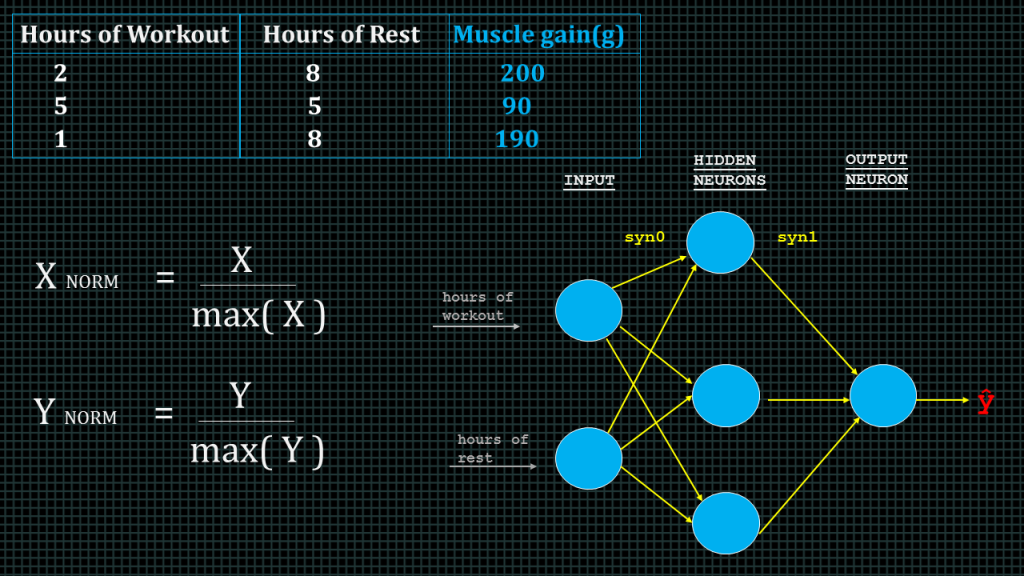
Lets say you want to design a neural network to predict how much muscles you gain given how many hours you workout and how many hours you rest.
Lets say you recorded the number of hours you worked out, the number of hours you rested and the muscles you gained in last 3 workout sessions and you want to use this data to train your neural network. This table here represents that data.
Once your model is properly trained you will simply enter the number of hours you want to workout tomorrow and the number of hours you want rest to rest tomorrow and it will predict how muscles you will gain, lets say are coder and professional body builder and you want to use this to optimize your body building.
This is called a supervised regression problem. It’s supervised because our examples have inputs and outputs. It’s a regression problem because we’re predicting your muscle gain, which is a continuous output. If we we’re predicting your mode as in whether happy or sad, this would be called a classification problem, and not a regression problem.
Before we throw our data into the model, we need to account for the differences in the units of our data. Both of our inputs are in hours, but our output is in grams. And the output values we are dealing with here are more than 10 times larger than the inputs. This will be a problem.
The solution is to scale our data, this way our model only sees standardized units. Here, we’re going to take advantage of the fact that all of our data is positive, and simply divide by the maximum value for each variable, effectively scaling the result between 0 and 1.
X here represents our inputs, that is hours of workout and hours of rest. Y represents our output which is muscle gain.
Now we can build our Neural Net. We know our network must have 2 inputs and 1 output, because these are the dimensions of our data. We’ll call our output y hat, because it’s an estimate of y, but not the same as y. Any layer between our input and output layer is called a hidden layer.
Here, we’re going to use 1 hidden layer with 3 hidden units, but if we wanted to build a deep neural network, we would just stack a bunch of layers together. Circles in our neural network represent neurons and lines represent synapses. Synapses have a really simple job, they take a value from their input, multiply it by a specific weight, and output the result
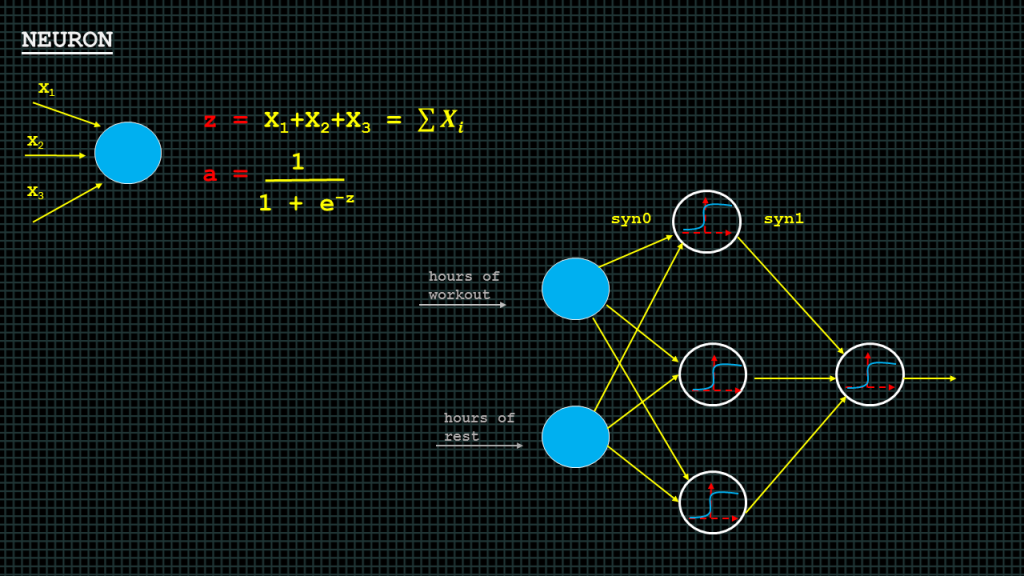
The neuron add together the outputs of all their synapses, and apply an activation function. Certain activation functions allow neural nets to model complex non-linear patterns, that simpler models may miss. We shall deal with various activation functions later on in the course.
“a” here is the activation function we shall apply to the output of our neuron. “z” represents the results from the neuron. Each capital “X” represents the results coming from each synapses the synapse result is computed my multiplying the input by a weight. The weight is not indicated in this slide.
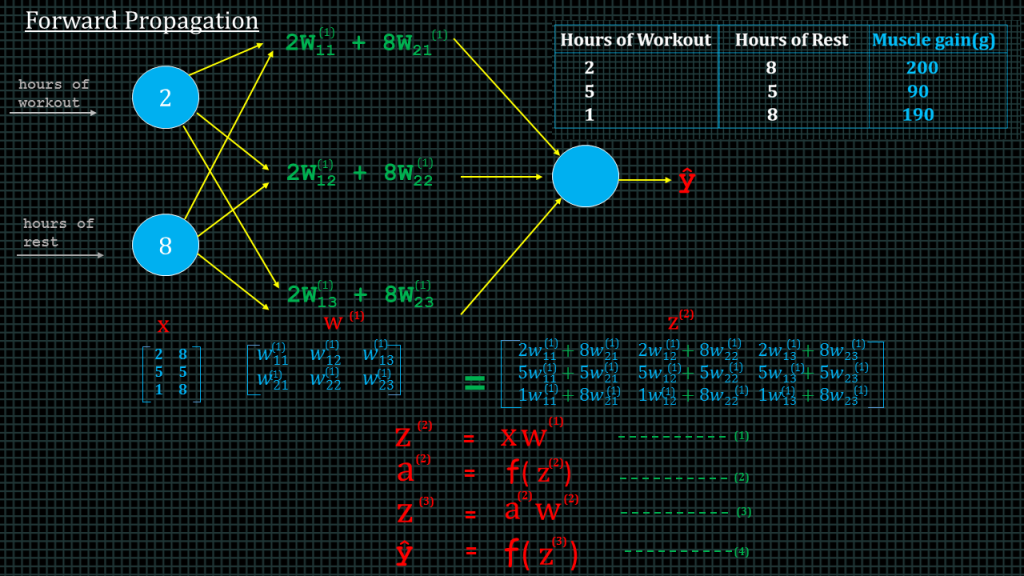
Each input value, or element in matrix X, needs to be multiplied by a corresponding weight and then added together with all the other results for each neuron. This is a complex operation, but if we take the three outputs we’re looking for as a single row of a matrix, and place all our individual weights into a matrix of weights, we can create the exact behavior we need by multiplying our input data matrix by our weight matrix. Using matrix multiplication allows us to pass multiple inputs through at once by simply adding rows to the matrix X. We shall spend a lot of time in this course talking about how to understand the dimensions of these types of matrices and how to multiply them.
For now, Notice that each entry in matrix z2 is a sum of weighted inputs to each hidden neuron. Z2 is of size 3 by 3, one row for each example, and one column for each hidden unit.
Z2 is the matrix multiplication of the inputs and their corresponding weight to the hidden layer. A2 is obtained by applying our activation function to z2.
Z3 is computed by multiplying the results of a2 by the weight of the synapse connecting the hidden layer to the output layer.
And finally yhat is obtained by applying our activation function to z3.
These 4 equations make up what is known as forward propagation. We have only for equations over here for forward propagation because our neural network has only one hidden layer. Later on in the course we will see how to determine the number of equations for forward propagation given an arbitrarily large neural network.
After forward propagation our neural network will undergo gradient descent then back propadation in order to update the weights.
We shall conclude this example here.
In the next example we shall design the entire neural network, from forward propagation through gradient descent to back propagation. These lessons were just to serve as an introduction to nueral network.

Add Comment